Question

Find k so that the line x+y=k is a tangent to the circle x²+y²=9​

Answer 1

The values of k so that the line x + y = k is a tangent to the circle x² + y² = 9​ are:

• k = 3√2
• k = -3√2

Explanation:

A tangent line to a circle intersects the circle at exactly one point.

Rearrange the equation of the tangent line to isolate y:

`\implies y=-x+k`

Substituting this into the equation of the circle gives a quadratic equation in the x-coordinates of the points of intersection:

`\implies x^2+(-x+k)^2=9`

`\implies x^2+x^2-2kx+k^2=9`

`\implies 2x^2-2kx+k^2-9=0`

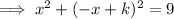
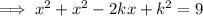
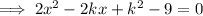
As we want this equation to have exactly one real solution, we can use the discriminant to find the value of k.

`\boxed{\begin{minipage}{7.6 cm}\underline{Discriminant}\\\\$b^2-4ac$ \quad when $ax^2+bx+c=0$\\\\when $b^2-4ac > 0 \implies$ two real solutions.\\when $b^2-4ac=0 \implies$ one real solution.\\when $b^2-4ac < 0 \implies$ no real solutions.\\\end{minipage}}`

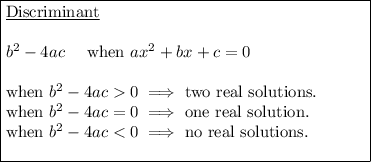
Substitute a = 2, b = -2k and c = (k² - 9) into the discriminant formula and set it equal to zero:

`\implies (-2k)^2-4(2)(k^2-9)=0`

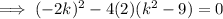
Solve for k:

`\implies 4k^2-8(k^2-9)=0`

`\implies 4k^2-8k^2+72=0`

`\implies -4k^2+72=0`

`\implies -4(k^2-18)=0`

`\implies k^2-18=0`

`\implies k^2=18`

`\implies k=\pm √(18)`

`\implies k=\pm √(9 \cdot 2)`

`\implies k=\pm √(9)√(2)`

`\implies k=\pm 3√(2)`

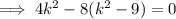
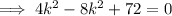
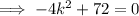
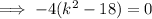
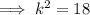
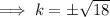
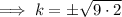
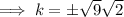
Therefore, the values of k so that the line x + y = k is a tangent to the circle x² + y² = 9​ are:

• k = 3√2
• k = -3√2