Question

2.3 moles of gas are contained in a balloon with a volume of 1.8 liters. What is the new volume of the balloon if the total moles inside are increased to 4.5 moles?

Answer 1

`\blue{\huge {\mathrm{COMBINED \; GAS \; LAW}}}`

`\\`

`{===========================================}`

`{\underline{\huge \mathbb{Q} {\large \mathrm {UESTION : }}}}`

• 2.3 moles of gas are contained in a balloon with a volume of 1.8 liters. What is the new volume of the balloon if the total moles inside are increased to 4.5 moles?

`{===========================================}`

`{\underline{\huge \mathbb{A} {\large \mathrm {NSWER : }}}}`

• The new volume of the balloon if the total moles inside are increased to 4.5 moles would be 3.52 liters.

`{===========================================}`

`{\underline{\huge \mathbb{S} {\large \mathrm {OLUTION : }}}}`

We can use the combined gas law to solve this problem:

• 
  `\sf((P_1 \cdot V_1))/(n_1) = ((P_2 \cdot V_2))/(n_2)`

where

• 
  `\sf P_1`,
  `\sf V_1`, and
  `\sf n_1` are the initial pressure, volume, and number of moles, and
• 
  `\sf P_2`,
  `\sf V_2`, and
  `\sf n_2` are the final pressure, volume, and number of moles.

We can rearrange this equation to solve for
`\sf V_2`:

• 
  `\sf V_2 = ((P_1 \cdot V_1 \cdot n_2))/((n_1 \cdot P_2))`

Plugging in the given values, we get:

• 
  `\sf V_2 = ((1\: atm \cdot 1.8\: L \cdot 4.5\: mol))/((2.3\: mol \cdot 1\: atm))`

Solving for
`\sf V_2`, we get:

• 
  `\bold{V_2 = \boxed{\bold{\:3.52\: L\:}}}`

Therefore, the new volume of the balloon if the total moles inside are increased to 4.5 moles would be 3.52 liters.

`{===========================================}`

`- \large\sf\copyright \: \large\tt{AriesLaveau}\large\qquad\qquad\qquad\qquad\qquad\qquad\tt 04/02/2023`

Answer 2

The new volume of the balloon sample if the total moles inside are increased to 4.5 moles is approximately 3.52 L (3 s.f.).

Step-by-step explanation:

As the temperature and pressure are constant, we can use Avogadro's Law to find the new volume.

Avogadro's Law

`\boxed{\sf (V_1)/(n_1)=(V_2)/(n_2)}`

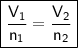
where:

• V₁ is the initial volume.
• n₁ is the initial number of moles.
• V₂ is the final volume.
• n₂ is the final number of moles.

Given 2.3 moles of gas are contained in a balloon with a volume of 1.8 liters, and the final number of moles is increased to 4.5 moles:

• V₁ = 1.8 L
• n₁ = 2.3 mol
• n₂ = 4.5 mol

Substitute the values into the formula and solve for V₂:

`\implies \sf (1.8\;L)/(2.3\;mol)=(V_2)/(4.5\;mol)`

`\implies \sf (1.8\;L)/(2.3\;mol)\cdot 4.5\;mol=(V_2)/(4.5\;mol) \cdot 4.5\;mol`

`\implies \sf V_2=(1.8\;L\cdot 4.5\;mol)/(2.3\;mol)`

`\implies \sf V_2=3.5217391...\;L`

`\implies \sf V_2=3.52\;L\;(3\;s.f.)`

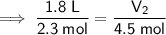
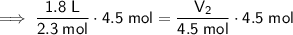
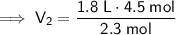
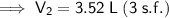
Therefore, the new volume of the balloon sample if the total moles inside are increased to 4.5 moles is approximately 3.52 L (3 s.f.).