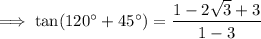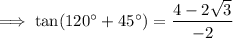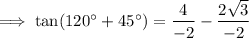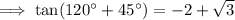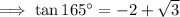Answer:
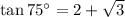
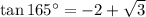
Explanation:
Tangent addition formula
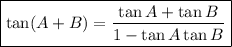
To evaluate tan 75°, we can use the tangent addition formula.
If A + B = 75° and 30° + 45° = 75°, then:
Substitute these values into the formula:
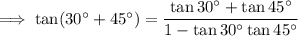
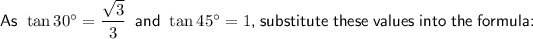
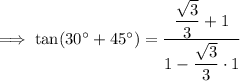
Simplify:
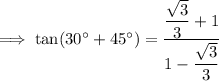
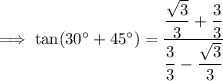
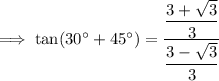
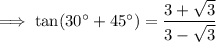
To rationalize the denominator, multiply the numerator and denominator by the conjugate of the denominator:
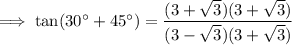
Simplify:
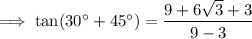
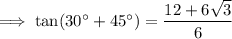
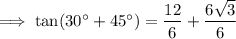
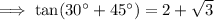
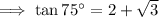

To evaluate tan 165°, we can use the tangent addition formula.
If A + B = 165° and 120° + 45° = 165°, then:
Substitute these values into the formula:
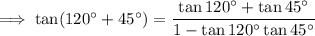
As tan 120° = -√3 and tan 45° = 1, substitute these values into the formula:
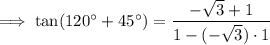
Simplify:
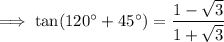
To rationalize the denominator, multiply the numerator and denominator by the conjugate of the denominator:
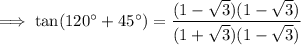
Simplify: