Question

Find the formula for an exponential function that passes through the two points given.

(x, y) = (0,5) and (x, y) = (3, 40)

Answer 1

`f(x)=5 \cdot 2^x`

Explanation:

The general form of an exponential function is:

`\boxed{f(x)=ab^x}`

where:

• a is the initial value (y-intercept).
• b is the base (growth/decay factor) in decimal form.

Substitute point (0, 5) into the equation and solve for a:

`\begin{aligned}(0,5) \implies ab^0&=5\\ a \cdot 1&=5\\a&=5\end{aligned}`

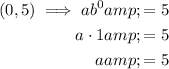
Now substitute point (3, 40) and the found value of "a" into the equation and solve for b:

`\begin{aligned}(3, 40) \implies 5 \cdot b^3&=40\\b^3&=8\\b^3&=2^3\\b&=2 \end{aligned}`

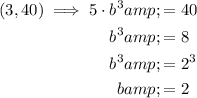
Therefore, the formula for an exponential function that passes through the points (0, 5) and (3, 40) is:

`f(x)=5 \cdot 2^x`