Question

ANWSER FOR QUESTION 5

PROVE OR DISPROVE RECT~SQUA

(100 points)

Answer 1

They are equal because
RECT is 18 and 10.5
SQUA is 6 and 3.5
If you multiply SQUA by 3
It equals to 18 and 10.5 which is the same as RECT

Answer 2

RECT is similar to SQUA since their corresponding angles are the same size, and the side lengths of RECT are three times the corresponding side lengths of SQUA (their corresponding sides are in the same ratio).

Explanation:

In similar shapes:

• Corresponding angles are the same size.
• Corresponding sides are always in the same ratio.

Since RECT and SQUA are both rectangular, their corresponding angles are the same size.

If RECT is similar to SQUA then their corresponding sides will be in the same ratio:

`\implies \sf RE:EC=SQ:QU`

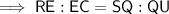
From inspection of the given diagram:

• RE = 18
• EC = 10.5
• SQ = 6
• QU = 3.5

Substitute these values into the ratio:

`\implies \sf 18:10.5=6:3.5`

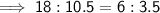
Therefore:

`\implies \sf (18)/(10.5)=(6)/(3.5)`

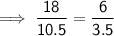
Cross multiply:

`\implies \sf 18 \cdot 3.5 = 6 \cdot 10.5`

`\implies \sf 63=63`

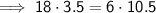
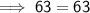
As the equation is true, this proves that RECT ~ SQUA.

Note: The side lengths of RECT are three times the corresponding side lengths of SQUA.