Question

Solve for x. Round to the nearest tenth.

x =


(40 points)

Answer 1

• 
  `x = 18.5`

Explanation:

To find:-

• The value of "x" .

Answer:-

We are given a right angled triangle, in which two legs viz perpendicular and base are x and 15 , and one of the angles is 51° .

With respect to 51° ,

• 15 is base .
• x is perpendicular .

Also , in a right angled triangle, tangent is defined as the ratio of perpendicular and base. So ,

`\implies \tan\theta =(p)/(b) \\`

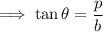
On substituting the respective values, we have;

`\implies \tan\theta =(x)/(15)\\`

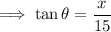
• Value of theta is 51° , so that ;

`\implies \tan51^o = (x)/(15) \\`

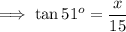
• Value of tan51° is approximately 1.2349 .

`\implies 1.2349 =(x)/(15) \\`

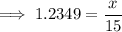
Cross multiply,

`\implies x = 15\cdot 1.2349 \\`

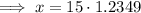
Simplify,

`\implies x = 18.5235 \\`

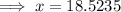
Rounding off to nearest tenth will give us,

`\implies \boxed{ x = 18.5 } \\`

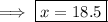
Hence the value of x is 18.5 ( nearest tenth) .