Question

The difference of two numbers is 17, and their product is 984. What are the two numbers?

Answer 1

Well based on trial and error of simultaneously dividing 984 by an even number. I was able to come across dividing 984 by 24 which gave me 41; I then subtracted it by 24 and got 17 so the answer to the question is 41 and 24

Answer 2

41 and 24 or -24 and -41

Explanation:

Let's assume that the first number is x and the second one is y.

Let's make two equations and put them in a system:

{x - y = 17,

{x × y = 984;

Let's make x the subject from the 1st equation:

x = 17 + y

Let's replace x in the 2nd equation:

(17 + y) × y = 984

`17y + {y}^(2) = 984`

`{y}^(2) + 17y - 984 = 0`

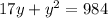
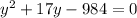
a = 1, b = 17, c = -984

Now, let's solve this quadratic equation:

`d = {b}^(2) - 4ac = {17}^(2) - 4 * 1 * ( - 984) = 289 + 3936 = 4225 > 0`

`y1 = ( - b - √(d) )/(2a) = ( - 17 -65 )/(2 * 1) = ( - 82)/(2) = - 41`

`y2 = ( - b + √(d) )/(2a) = ( - 17 + 65)/(2 * 1) = (48)/(2) = 24`

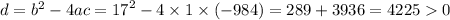
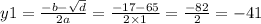
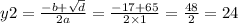
No matter which y we choose (y1 or y2) the equations in the system will be correct:

If we choose y2:

x2 = 17 + y2

x2 = 17 + 24 = 41

{x - y = 17,

{41 - 24 = 17;

{x × y = 984,

{41 × 24 = 984;

If we choose y1:

x1 = 17 + y1

x1 = 17 + (-41) = -24

{x - y = 17,

{-24 - (-41) = -24 + 41 = 17;

{x × y = 984,

{-24 × (-41) = 984;

So the two possible number are:

41 and 24

-24 and -41