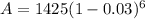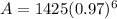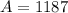Question

The student population at

a high school is 1,425 and
decreases by 3% each
year. What will the student
population be after 6
years?

Answer 1

the student population will be 1187 after 6 years

Explanation:

The rate at which the population is decreasing is exponential. We would apply the exponential decay formula which is expressed as

`A = P(1 - r)^t`

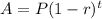
Where

A represents the population after t years.

t represents the number of years.

P represents the initial population.

r represents rate of decrease.

From the information given,

`P = 1425`

`r = 3\% = (3)/(100) = 0.03`,

`t = 6 \ \text{years}`

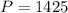
Therefore,

`A = 1425(1 - 0.03)^6`

`A = 1425(0.97)^6`

`A = 1187`

Answer 2

1,1685

Explanation:

First, we have to find how much the population decreases each year (find 3% of the number 1,425):

`(1.425 * 3\%)/(100\%) = 0.04275`

Now, that we know how much it decreases each year.

We have to multiply this number by 6 to find how much it will decrease after 6 years:

0,04275 × 6 = 0,2565

Now, subtract this number from the earlier number (1,425) to find the population after 6 years:

1,425 - 0,2565 = 1,1685