Using the quadratic formula, solve the equation below to find the two values of x. 8x^(2) - 35 = -18x Give each value as a fraction in it's simplest form.

Question

Using the quadratic formula, solve the equation below to find the two values of x.


`8x^(2) - 35 = -18x`
Give each value as a fraction in it's simplest form.

Answer 1

To solve the equation
`8x^2 - 35 = -18x` using the quadratic formula, we can first rearrange it into standard quadratic form:

`8x^2 + 18x - 35 = 0`

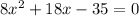
The quadratic formula is:

x = [-b ± sqrt(b^2 - 4ac)] / 2a

where a, b, and c are the coefficients of the quadratic equation. In this case:

a = 8, b = 18, and c = -35

Substituting these values into the formula, we get:

x = [-18 ±
`sqrt(18^2 - 4(8)(-35))] / 2(8)`

Simplifying the expression inside the square root:

x = [-18 ± sqrt(324 + 1120)] / 16

x = [-18 ± sqrt(1444)] / 16

x = [-18 ± 38] / 16

So the two solutions are:

x = (-18 + 38) / 16 = 1/2 or x = (-18 - 38) / 16 = -7/4

Explanation:

Therefore, the two values of x as fractions in their simplest forms are 1/2 and -7/4.

Answer 2

Answer:
x=5/4 or x= -7/2

Explanation:
Please click on the picture to see the explanation clearly!