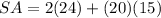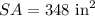Question

ASAP!! ITS URGENT

If the base of a right prism is a rhombus whose diagonals are 6 km and 8 km and
whose altitude is 15 km, then the volume of the prism is…

Answer 1

The total surface area of the prism is
`SA=348 \ \text{in}^2`

Explanation:

we know that

The two diagonals of a rhombus are perpendicular and bisect each other

All sides are congruent

The surface area of a prism is equal to

`SA=2B+Ph`

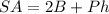
where

B is the area of the base of prism

P is the perimeter of the base of prism

h is the height of the prism

step 1

Find the length side of the rhombus

Applying Pythagoras Theorem

`c^2=a^2+b^2`

we have

c is the length side of the rhombus

a and b are the semi diagonals of the rhombus

`a=8/2=4 \ \text{in}`

`b=6/2=3 \ \text{in}`

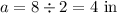
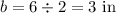
substitute

`c^2=4^2+3^2`

`c^2=25`

`c=5 \ \text{in}`

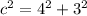
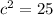
step 2

Find the perimeter of the base P

The perimeter of the rhombus is equal to

`P=4c`

`P=4(5)=20 \ \text{in}`

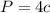
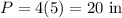
step 3

Find the area of the base B

The area of the rhombus is

`B=(1)/(2)[D1* D2]`

D1 and D2 are the diagonals of the rhombus

substitute

`B=(1)/(2)[8* 6]=24 \ \text{in}^2`

step 4

Find the surface area of the prism

`SA=2B+Ph`

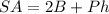
substitute the values

`SA=2(24)+(20)(15)`

`SA=348 \ \text{in}^2`