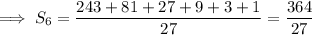Question

Find the sum of the series 9 +3+1+...+1/27​

Answer 1

`(364)/(27)`

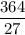
Explanation:

A geometric sequence has a constant ratio (multiplier) between each term, so each term is multiplied by the same number, whereas an arithmetic sequence has a constant difference between each term, so the difference between each term is the same.

Given series:

• 9 + 3 + 1 + ... + 1/27​

As each term of the given sequence is a third of the previous term, the given series is a geometric series. This means the common ratio (r) is 1/3.

From inspection of the given series, the first term (a) is 9.

To find the value of n for the nth term 1/27, simply divide each term by 3:

`a_1=9`

`a_2=(a_1)/(3)=(9)/(3)=3`

`a_3=(a_2)/(3)=(3)/(3)=1`

`a_4=(a_3)/(3)=(1)/(3)`

`a_5=(a_4)/(3)=((1)/(3))/(3)=(1)/(9)`

`a_6=(a_5)/(3)=((1)/(9))/(3)=(1)/(27)`

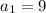
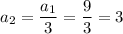
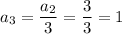
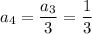
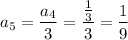
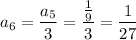
Therefore, as the 6th term in the sequence is 1/27, we need to find the sum of the series of the first 6 terms. To do this, use the geometric series formula.

`\boxed{\begin{minipage}{7 cm}\underline{Sum of the first $n$ terms of a geometric series}\\\\$S_n=(a(1-r^n))/(1-r)$\\\\where:\\\phantom{ww}$\bullet$ $a$ is the first term. \\ \phantom{ww}$\bullet$ $r$ is the common ratio.\\\end{minipage}}`

The given values are:

• a = 9
• r = 1/3
• n = 6

Substitute these values into the formula to find the sum of the first 6 terms:

`\implies S_n=(a(1-r^n))/(1-r)`

`\implies S_6=(9\left(1-(1)/(3)^6\right))/(1-(1)/(3))`

`\implies S_6=(9\left(1-(1)/(729)\right))/((2)/(3))`

`\implies S_6=(9\left((728)/(729)\right))/((2)/(3))`

`\implies S_6=((728)/(81))/((2)/(3))`

`\implies S_6=(728)/(81) \cdot (3)/(2)`

`\implies S_6=(2184)/(162)`

`\implies S_6=(364)/(27)`

`\hrulefill`

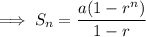
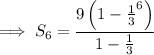
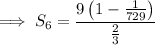
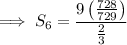
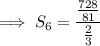
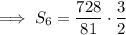
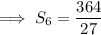
Alternative method

As there are only 6 terms to sum, an alternative method would be to simply add the 6 terms:

`\implies S_6=9+3+1+(1)/(3)+(1)/(9)+(1)/(27)`

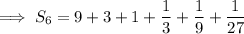
Rewrite all the numbers so that they are fractions with the same denominator of 27:

`\implies S_6=(243)/(27)+(81)/(27)+(27)/(27)+(9)/(27)+(3)/(27)+(1)/(27)`

As the denominators are the same, simply add the numerators:

`\implies S_6=(243+81+27+9+3+1)/(27)=(364)/(27)`