Question

Use the information given below to find cos(α+β)

Answer 1

`\cos(\alpha + \beta)=-(171)/(221)`

Explanation:

We can find cos(α + β) by using the trigonometric identity:

`\boxed{\cos(\alpha +\beta)=\cos \alpha \cos \beta - \sin \alpha \sin \beta}`

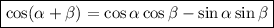
Therefore, we need to find cos α and cos β.

To find the cosine of an angle given the sine of an angle, we can use the identity:

`\boxed{\sin^2 \theta + \cos^2 \theta=1}`

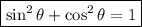
Rearrange the original identity to isolate cos θ:

`\implies \cos \theta=√(1-\sin^2 \theta)`

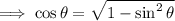
Substitute the given values of sin α and sin β into the rearranged identity to find the value of cos α and cos β:

`\begin{aligned}\implies \cos \alpha&=√(1-\sin^2 \alpha)\\\\&=\sqrt{1-\left(-(12)/(13)\right)^2}\\\\&=\sqrt{1-(144)/(169)}\\\\&=\sqrt{(25)/(169)}\\\\&=(5)/(13)\end{aligned}`
`\begin{aligned}\implies \cos \beta&=√(1-\sin^2 \beta)\\\\&=\sqrt{1-\left(-(8)/(17)\right)^2}\\\\&=\sqrt{1-(64)/(289)}\\\\&=\sqrt{(225)/(289)}\\\\&=(15)/(17)\end{aligned}`

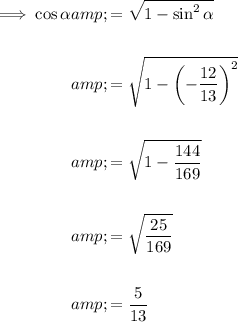
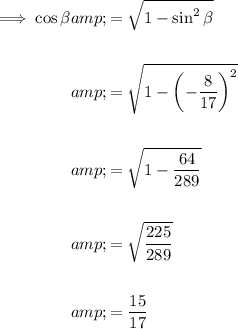
Cosine is negative in Quadrants II and III, and positive in Quadrants I and IV.

Therefore, as angle α is in Quadrant III, cos α is negative:

`\implies \cos \alpha = -(5)/(13)`

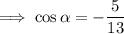
Therefore, as angle β is in Quadrant IV, cos β is positive:

`\implies \cos \beta=(15)/(17)`

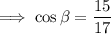
Finally, substitute the values into the identity cos(α + β):

`\begin{aligned}\implies\cos(\alpha + \beta)&=\cos \alpha \cos \beta - \sin \alpha \sin \beta}\\\\&=\left(-(5)/(13)\right)\cdot (15)/(17) - \left(-(12)/(13)\right) \cdot \left(-(8)/(17)\right)\\\\&=-(75)/(221)-(96)/(221)\\\\&=-(171)/(221)\end{aligned}`

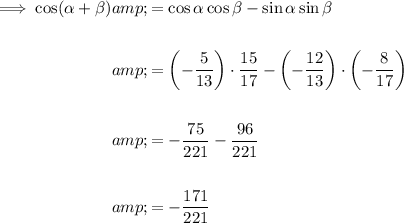
Solution

Therefore, the exact answer is:

`\cos(\alpha + \beta)=-(171)/(221)`