Question

Fine bc

(100 points)

Answer 1

• 
  `BC = 32.96`

Explanation:

To find:-

• The value of BC .

Answer:-

We are given a triangle with two angles as 93° and 58°. Firstly let's find out the third angle of the triangle using angle sum property of triangle .

Angle sum property of triangle:-

• The sum of all interior angles of any triangle is 180° .

If three angles are
`a` ,
`b` and
`c` , then ;

`\longrightarrow\boxed{ A + B + C = 180^o} \\`

On substituting the respective values, we have;

`\longrightarrow 93^o + 58^o + B = 180^o \\`

`\longrightarrow 151^o + B = 180^o \\`

`\longrightarrow B = 180^o - 151^o \\`

`\longrightarrow B = 29^o\\`

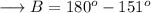
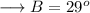
Secondly, we can use Law of Sines to find out the value of BC. If we denote side BC by "a" , AB by "c" and AC by "b" , then we can say that,

Law of sines :-

`\longrightarrow \boxed{ (a)/(\sin A )=(b)/(\sin B )=(c)/(\sin C ) } \\`

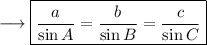
Now we can see that in the given triangle,

• AC = b = 16
• B = 29°
• BC = a = ?
• A = 93°

So that ,

`\longrightarrow (a)/(\sin A )=(b)/(\sin B ) \\`

`\longrightarrow (a)/(\sin 93^o )=(b)/(\sin 29^o)\\`

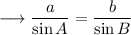
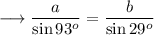
• Value of sin93° is approximately 0.9986 .
• Value of sin29° is approximately 0.4848 .

On substituting the respective values, we have;

`\longrightarrow (a)/(0.9986)=(16)/(0.4848) \\`

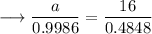
Simplify and solve for "a" ,

`\longrightarrow a =(16\cdot 0.9986)/(0.4848) \\`

`\longrightarrow a = 32.9570\\`

`\longrightarrow \underline{\underline{ \red{ BC = 32.96 }}} \\`

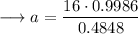
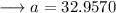
Hence the value of BC is 32.96 approximately.

Answer 2

• 32.95 or 33 units (rounded)

----------------------------------

Use the law of sines to find the missing side length.

First, find the angle B opposite to know side AC = 16, using angle sum property for the triangle:

• m∠B = 180° - (58° + 93°) = 29°

Find the missing side length, using ratios below:

• AC / sin B = BC / sin A
• 16/ sin 29 = BC / sin 93
• BC = 16 sin 93 deg / sin 29 deg
• BC = 32.95 ≈ 33 units (rounded)