Question

100 POINTS!

Factor completely.
(-a^2)+(ab)+(2b^2)
You have to use the box method.

(Algebra 1)

Answer 1

Explanation:

I am not sure of the box method but here is an answer that maybe you can adapt

(-a+b)(a+b) = - a^2 - ab + ab + b^2 = - a^2 + b^2

now we need to add (b^2 and ab) to this to get the answer given

- a^2 + b^2 + b^2 + ab this will give the result needed ..factor it

( -a+b)(a+b) + b^2 + ab

( b-a)(a+b) + b ( b+a) this DOES equal -a^2 + ab + 2b^2

This can then be further reduced ( due to the common factor (b+a) to ( 2b-a)(a+b)

Answer 2

(-a + 2b)(a + b)

Explanation:

Given trinomial:

`(-a^2)+(ab)+(2b^2)`

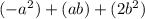
To factor using the box method, first create a 2x2 grid.

Place the first term of the trinomial in the upper left box, and the last term in the bottom right box of the 2x2 grid:

`\begin{array}\cline{1-2}\vphantom{\frac12}-a^2&\\\cline{1-2}\vphantom{\frac12}&2b^2\\\cline{1-2}\end{array}`

Multiply these two terms together:

`-a^2 * 2b^2=-2a^2b^2`

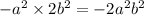
Look for factors of -2a²b² that will sum to the second term of the trinomial, ab.

Factors of -2a²b² that sum to ab are: -ab and 2ab.

Place -ab and 2ab in the empty boxes of the grid (the order doesn't matter):

`\begin{array}\cline{1-2}\vphantom{\frac12}-a^2&-ab\\\cline{1-2}\vphantom{\frac12}2ab&2b^2\\\cline{1-2}\end{array}`

Find the greatest common factor of each row and write them down on the outside of the box.

`\begin{array}c\cline{2-3}\vphantom{\frac12}-a&-a^2&-ab\\\cline{2-3}\vphantom{\frac12}2b&2ab&2b^2\\\cline{2-3}\end{array}`

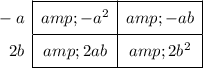
Find the greatest common factor of each column and write them down on the outside of the box.

`a\quad\;\;\;\;b`

`\begin{array}c\cline{2-3}\vphantom{\frac12}-a&-a^2&-ab\\\cline{2-3}\vphantom{\frac12}2b&2ab&2b^2\\\cline{2-3}\end{array}`

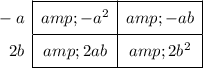
The factors of the trinomial are the sum of the external column numbers and the sum of the external row numbers: (-a + 2b) and (a + b).

Therefore, (-a²) + (ab) + (2b²) factored completely using the box method is:

• (-a + 2b)(a + b)