Question

A community center sells a total of 295 tickets for a basketball game. An adult ticket costs $4. A student ticket costs $1. The sponsors

collect $574 in ticket sales. Find the number of each type of ticket sold.
The number of adult tickets sold should be ____and the number of student tickets sold should be _____
(Simplify your answers.)

Answer 1

93 adult tickets; 202 student tickets

Explanation:

We can solve for the number of adult and student tickets using a system of equations.

We know that (adult ticket cost * quantity) + (student ticket cost * quantity) = total revenue and that the total # of adult tickets + total # of student tickets = total number of tickets.

Thus, our two equations are 4A + S = 574 and A + S = 295.

We can solve using substitution and first isolate A in the second equation to get A = -S + 295

Now, we can substitute A into the first equation and solve for S:

`4(-S+295)+S=574\\-4S+1180+S=574\\-3S+1180=574\\-3S=-606\\S=202`

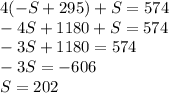
Since we now know that S = 202, we can solve for A using the second equation and simply subtract 202 from 295

A + 202 = 295

A = 93