Answer:
Approximately
 and approximately
and approximately
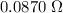 .
.
Step-by-step explanation:
Since the emf of
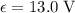 is divided between
is divided between
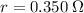 and
and
 , the current in this circuit would be:
, the current in this circuit would be:
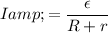 .
.
The resistor
 would dissipate:
would dissipate:
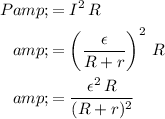 .
.
Rearrange this equation to obtain:
 .
.
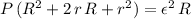 .
.
 .
.
Given that
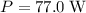 :
:
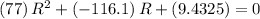 .
.
Solve this quadratic equation of
 using the quadratic formula to obtain:
using the quadratic formula to obtain:
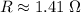 or
or
 .
.
(Substitute each value into the equation
 to verify the results.)
to verify the results.)