Question

Find the center and radius of the circle represented by the equation below.

Answer 1

• Center = (6,1)
• radius = 19 units

Explanation:

To find:-

• The centre and radius of the circle.

Answer:-

The standard equation of circle is ,

`\longrightarrow (x-h)^2+(y-k)^2=r^2 \\`

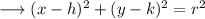
where ,

• (h,k) is centre.
• r is the radius.

The given equation to us is,

`\longrightarrow (x-6)^2+(y-1)^2=361 \\`

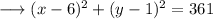
This can be rewritten as ,

`\longrightarrow (x-6)^2 +(y-1)^2=19^2 \\`

On comparing it to the standard equation of the circle , we can clearly see that ,

`\longrightarrow \red{ \rm{Centre} = (6,1)} \\`

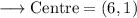
And ,

`\longrightarrow \red{\rm{radius}= 19 \ \rm{units}} \\`

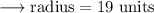
This is the required answer.

Answer 2

centre = (h,k) = (6,1)

radius = 19

Explanation:

(x-6)^2 + (y-1)^2 = 361

or, (x-6)^2 + (y-1)^2 = 19^2

Comparing with (x-h)^2 +(y-k)^2 = r^2

We get,

h=6

k=1

r=19

therefore, centre = (h,k) = (6,1)

radius = 19