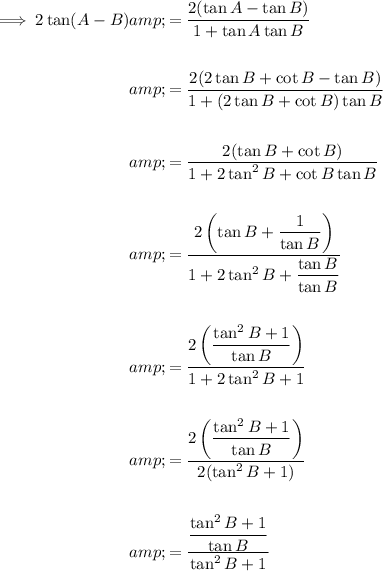Answer:
See below for proof.
Explanation:
Trigonometric identity

Using the above trigonometric identity, we can rewrite 2 tan (A - B) as:

Given that 2 tan B + cot B = tan A, substitute this into the fraction:
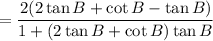
Simplify:


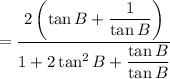
Simplify:
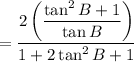
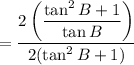
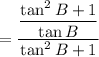

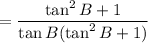
Cancel the common factor (tan²B + 1):
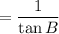

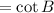

As one calculation: