Question

If A+B = Pi radian /4 then show that
​

Answer 1

See below for proof.

Explanation:

Begin by using the trigonometric identity:

`\boxed{\tan(A+B) = (\tan A + \tan B)/(1 - \tan A \tan B)}`

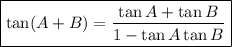
Given that A + B = π/4, then:

`\tan\left((\pi)/(4)\right) = (\tan A + \tan B)/(1 - \tan A \tan B)`

Since tan(π/4) = 1, we can simplify the equation to:

`1= (\tan A + \tan B)/(1 - \tan A \tan B)`

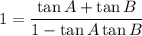
Multiply both sides by (1 - tan A tan B):

`1 - \tan A \tan B=\tan A + \tan B`

Add tan A tan B to both sides of the equation:

`1=\tan A +\tan B+ \tan A \tan B`

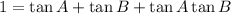
Rearrange:

`\tan B + \tan A\tan B+\tan A=1`

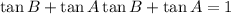
Add 1 to both sides of the equation:

`\tan B + \tan A\tan B+1+\tan A=2`

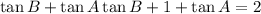
Factor out the common term tan B from the first two terms:

`(1+\tan A)\tan B+1+\tan A=2`

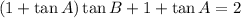
Rewrite as:

`(1+\tan A)\tan B+1(1+\tan A)=2`

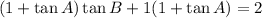
Factor out the common term (1 + tan A):

`(1+\tan A)(1 + \tan B)=2`

Therefore, we have shown that (1 + tan A)(1 + tan B) = 2 when A + B = π/4.