Question

A flexible container holding 4.00 moles of a gas contracts from 89.6 L to 44.8 L when some gas is released. How many moles of gas are in the reduced container?​

Answer 1

Answer:2.00

Step-by-step explanation:

Using the formula you provided, n2 = n1 * (V2 / V1). Plugging in the values, n2 = 4.00 mol * (44.8 L / 89.6 L), we find that n2 is approximately 2.00 moles. So, there are 2.00 moles of gas in the reduced container.

Answer 2

`\Huge \boxed{\boxed{\textbf{2.00 moles}}}`

Step-by-step explanation:

The number of moles of gas in the reduced container can be calculated using Avogadro's law, which states that the volume of a gas is directly proportional to the number of moles of the gas, assuming that the temperature and pressure remain constant.

Given that the initial volume of the gas was 89.6 L and it contained 4.00 moles, the volume per mole is:

`\boxed{\tt{ \frac{89.6 \, \texttt{L}}{4.00 \, \texttt{moles}} = 22.4 \, \texttt{L/mole}}}`

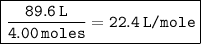
After the gas is released, the volume of the container is reduced to 44.8 L. The number of moles of gas in the reduced container can be calculated by dividing the reduced volume by the volume per mole:

`\boxed{\tt{\frac{44.8 \, \texttt{L}}{22.4 \, \texttt{L/mole}} = 2.00 \, \texttt{moles}}}`

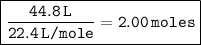
Therefore, there are 2.00 moles of gas in the reduced container.

#BTH1

________________________________________________________