Question

A tetherball on a 1.55-m rope is struck so that it goes into circular motion in a horizontal plane, with the rope making a 12.0° angle to the horizontal. Part A What is the ball's speed? Express your answer with the appropriate units. НА ?

Answer 1

Approximately
`5.40\; {\rm m\cdot s^(-1)}` (assuming that
`g = 9.81\; {\rm N \cdot kg^(-1)}`.)

Step-by-step explanation:

Refer to the diagram attached. There are two forces on this tetherball: tension
`T` in the string, and weight
`m\, g`- where
`m` is the mass of the tetherball.

Let
`T` denote the tension in the string, and let
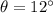`\theta = 12^(\circ)` denote the angle of elevation of this force. Decompose
`T\!` into two components: horizontal and vertical:

• Vertical:
  `T\, \sin(\theta)`, and
• Horizontal:
  `T\cos(\theta)`.

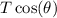The tetherball is moving in a horizontal plane, meaning that there is no motion in the vertical direction. Hence, the resultant force in the vertical direction should be
`0`. The vertical component of the tension
`T\, \sin(\theta)` should exactly balance the weight of the tetherball
`m\, g`:

`T\, \sin(\theta) = m\, g`.

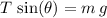Hence, the resultant (unbalanced) force on this tetherball would be equal to the horizontal component of tension:
`F_{\text{net}} = T\, \cos(\theta)`.

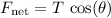The length of the rope is
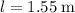`l = 1.55\; {\rm m}`. Since this rope is also at the angle of
`\theta` above the horizon, the radius of the circular motion in the horizontal plane would be
`r = l\, \cos(\theta)`.

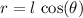Since the ball is in a centripetal motion, the resultant force on this ball would also be
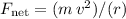`F_{\text{net}} = (m\, v^(2)) / (r)`, where
`v` is the velocity of the ball.

Equate these two expressions of
`F_{\text{net}}` to obtain:

`\displaystyle T\, \cos(\theta) = F_{\text{net}} = (m\, v^(2))/(r)`.

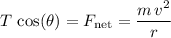Additionally,
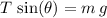`T\, \sin(\theta) = m\, g` since the forces on the vertical direction are balanced. Rewrite both this equation and the equation
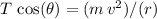`T\, \cos(\theta) = (m\, v^(2)) / (r)` to isolate tension
`T`:

`\left\lbrace \begin{aligned}& T\, \cos(\theta) = (m\, v^(2))/(r) \\ &T\, \sin(\theta) = m\, g\end{aligned}\right.`.

`\left\lbrace \begin{aligned}& T = (m\, v^(2))/(r\, \cos(\theta)) \\ &T = (m\, g)/(\sin(\theta))\end{aligned}\right.`.

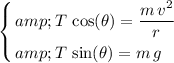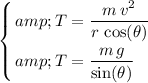Solve this system for velocity
`v`:

`\begin{aligned}(m\, v^(2))/(r\, \cos(\theta)) &= (m\, g)/(\sin(\theta))\end{aligned}`.

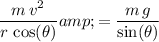Since
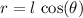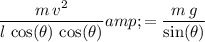`r = l\, \cos(\theta)`:

`\begin{aligned}(m\, v^(2))/(l\, \cos(\theta)\, \cos(\theta)) &= (m\, g)/(\sin(\theta))\end{aligned}`.

`\displaystyle (m\, v^(2))/(l\, \cos^(2)(\theta)) = (m\, g)/(\sin(\theta))`.

`\begin{aligned}v &= \sqrt{(g\, l\, \cos^(2)(\theta))/(\sin(\theta))} \\ &\approx \sqrt{(9.81\, (\cos(12^(\circ)))^(2))/((1.55)\, \sin(12^(\circ)))}\; {\rm m\cdot s^(-1)} \\ &\approx 5.40\; {\rm m\cdot s^(-1)}\end{aligned}`.