Question

Determine the equation of straight line which passes through the point (a, b)and perpendicular to ax+by=5

Answer 1

`y=(b)/(a) x.`

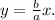
Explanation:

1) if the required straight line is 'l', the given point is A(a;b), then the required equation of line can be written in form:

`(x-a)/(x_1-a) =(y-b)/(y_1-b),`

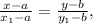
where (x₁;y₁) is other point B, which belongs to the 'l';

2) from the equation it is possible to detect the coordinates of the perpendicular, they are (x₁-a;y₁-b);

3) if the given perpendicular is ax+by=5, then the coordinates of the vector (a;b) are coordinates of the vector, which belongs to the required line 'l', and then: x₁-a=a and y₁-b=b;

4) if to substitute the a=x₁-a and b=y₁-b into the required equation of line 'l', then:

`(x-a)/(a) =(y-b)/(b);`

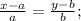
5) finally, the equation is: ay=bx, or y=b/a *x (slope-interception form).

note: the suggested solution is not the only way.