Question

Determine the equation of the circle graphed below.

Answer 1

`(x+6)^2+(y-5)^2=4^2`

Explanation:

To find:-

• Equation of the circle.

Answer:-

We are interested in finding out the equation of the given circle. For that , take any two diametrically opposite coordinates. Two such coordinates are (-6,1) and (-6,9) . Now using midpoint formula , find the midpoint as ,

Midpoint formula:-

`\longrightarrow \boxed{(x_m,y_m)=\left((x_1+x_2)/(2),(y_1+y_2)/(2)\right)}\\`

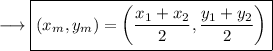
On substituting the respective values, we have;

`\longrightarrow (x_m,y_m) =\bigg((-6-6)/(2),(1+9)/(2)\bigg) \\`

`\longrightarrow (x_m,y_m) =\bigg((-12)/(2),(10)/(2)\bigg) \\`

`\longrightarrow \red{ (x_m,y_m) = (-6,5)}\\`

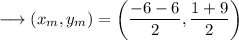
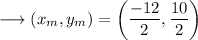
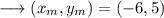
This is the coordinate of the centre of the circle as centre is at the midpoint of the diameter. Now using distance formula , we can find the radius. Here we will use the coordinates of the centre and any one of the point on the circle say (-6,1) .

Distance formula :-

`\longrightarrow \boxed{d =√((x_2-x_1)^2+(y_2-y_1)^2)} \\`

On substituting the respective values, we have;

`\longrightarrow d =\sqrt{ \{-6-(-6)\}^2+(5-1)^2}\\`

`\longrightarrow d =√( (-6+6)^2+4^2) \\`

`\longrightarrow d =√(0+4^2) \\`

`\longrightarrow d =√(4^2) \\`

`\longrightarrow \red{ d = 4 \ units } \\`

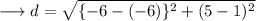
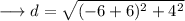
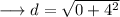
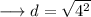
Hence the radius of the circle is 4 units.

Now we know the standard equation of circle , which is ,

`\longrightarrow (x-h)^2+(y-k)^2=r^2 \\`

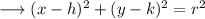
where ,

• 
  `(h,k)` is the centre.
• 
  `r` is the radius.

On substituting the respective values, we have;

`\longrightarrow \{ x-(-6)^2\}^2+(y-5)^2 = 4^2 \\`

`\longrightarrow \underline{\underline{ \red{ (x+6)^2+(y-5)^2 = 4^2}}}\\`

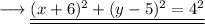
This is the required equation of the circle.