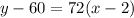Question

If ƒ'(x) = 9x√3x² +4 and ƒ(0) = 4 find the
equation of the line tangent to
f at x = 2.

Answer 1

`y - 60 = 72(x-2)`

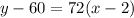
Explanation:

We need slope, an x coordinate, and a y coordinate for a tangent line.

Slope: f'(x) will give us the slope, so f'(2) = m = 9(2)
`√(3(2)^2 +4)` = 18(
`√(16)`) = 18(4) = 72

X coordinate: 2, given by the question.

Y coordinate: For the Y coordinate, we need to find f(2). To find f(x), we will use integration by substitution
`u = 3x^2`
`du =6x dx`

`\int\ {(9)/(6)√(u) } \, du`

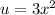
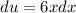
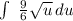
Apply Linearity

`(3)/(2) \int√(u) } \, du`

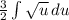
Integrate

`u^{(3)/(2)} + C`

Undo substitution

`(√(3x^2 + 4^)})^3 + C`

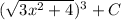
Plug in x = 0 and solve for C

`4 =√((3(0)^2 + 4)^3) + C \\4 = √(64) + C\\4 = 8 + C\\C = -4`

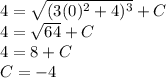
Now solve for f(2)

`(√(3(2)^2 + 4^)})^3 - 4`

`(√(16)})^3 - 4\\64 - 4\\60`

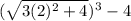
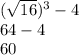
Fill in point slope form

`y - 60 = 72(x-2)`