Question

Suppose the demand d, in units sold, for a company's jeans at price x, in dollars, is d(x) = 400 - 4x.

a. If revenue = price x demand, write the rule for the
function r(x), which represents the company's
expected revenue in jean sales. Then state the
domain of this function.
b. If the price is $40, how much revenue will the
company earn?
Revenue
Price

Answer 1

a. The revenue function, r(x), is given by the product of the price x and the demand function d(x):

`\sf r(x) = x * d(x) = x * (400 - 4x) = 400x - 4x^2`

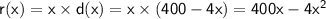
The domain of this function is the set of possible prices that can be charged for the jeans, which is typically a positive real number, or in interval notation: (0, infinity).

b. If the price is $40, we can find the revenue by plugging in x = 40 into the revenue function:

`\sf r(40) = 400(40) - 4(40)^2 = 16,000 - 6,400 = 9,600`

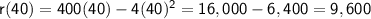
Therefore, the company will earn $9,600 in revenue if they sell their jeans at a price of 40