Question

A gas sample in a cylinder has a pressure of 0.75 atm at 15.00°C. What will

be the pressure of the gas be if the temperature increases to 50.00°C?
Ans:
atm

Answer 1

To solve this problem, we can use the combined gas law, which relates the pressure, volume, and temperature of a gas:

• 
  `((P_1V_1))/(T_1) = ((P_2V_2))/(T_2)`

where:

• 
  `P_1` and
  `T_1` are the initial pressure and temperature,
• 
  `P_2` is the final pressure,
• 
  `T_2` is the final temperature, and
• 
  `V_1` and
  `V_2` are the initial and final volumes (which we can assume to be constant in this case).

We can rearrange this equation to solve for
`P_2`:

• 
  `P_2 = ((P_1 * T_2 * V_1))/((T_1 * V_2))`

Since
`V_1` and
`V_2` are constant in this case, we can simplify this to:

• 
  `P_2 = ((P_1 * T_2))/((T1))`

Substituting the given values, we get:

• 
  `P_2 = ((0.75 \: atm * 323.15 \: K))/((288.15 \: K))`

where:

• we have converted the temperatures to Kelvin by adding 273.15.

Simplifying, we get:

• 
  `P_2 = 0.84 \: atm`

Therefore, the pressure of the gas will be 0.84 atm if the temperature increases to 50.00°C.

`\rule{200pt}{5pt}`

Answer 2

The final pressure is 0.841 atm (to three significant figures).

Step-by-step explanation:

Since the volume is unchanged, we can use Gay-Lussac's Law to find the pressure of the gas if the temperature increases to 50.00°C.

Gay-Lussac's Law

`\boxed{\sf (P_1)/(T_1)=(P_2)/(T_2)}`

where:

• P₁ is the initial pressure.
• T₁ is the initial temperature (measured in kelvin).
• P₂ is the final pressure.
• T₂ is the final temperature (measured in kelvin).

Rearrange the equation to solve for P₂:

`\implies \sf P_2=(P_1 \cdot T_2)/(T_1)`

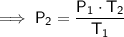
Convert Celsius to kelvin by adding 273.15:

`\implies \sf 15.00^(\circ)C=15.00+273.15=288.15\;K`

`\implies \sf 50.00^(\circ)C=50.00+273.15=323.15\;K`

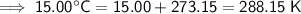
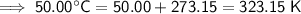
Therefore, the values to substitute into the formula are:

• P₁ = 0.75 atm
• T₁ = 288.15 K
• T₂ = 323.15 K

Substitute the values into the formula and solve for P₂:

`\implies \sf P_2=(0.75 \cdot 323.15)/(288.15)`

`\implies \sf P_2=0.841098...`

`\implies \sf P_2=0.841\;atm\;(3\;s.f.)`

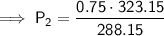
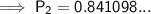
Therefore, the final pressure is 0.841 atm (to three significant figures).