Question

A boy on a 1.9 kg skateboard initially at rest

tosses a(n) 8.0 kg jug of water in the forward
direction.
If the jug has a speed of 2.7 m/s relative to
the ground and the boy and skateboard move
in the opposite direction at 0.65 m/s, find the
boy’s mass.
Answer in units of kg.

Answer 1

Approximately
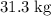`31.3\; {\rm kg}`. (Assuming the friction between the skateboard and the ground is negligible.)

Step-by-step explanation:

The momentum
`p` of an object of
`m` and velocity
`v` is:

`p = m\, v`.

When the boy tossed the jug of water, the change in the momentum of the jug would be:

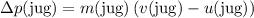`\Delta p(\text{jug}) = m(\text{jug}) \, (v(\text{jug}) - u(\text{jug}))`, where:

• 
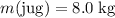  `m(\text{jug}) = 8.0\; {\rm kg}` is the mass of the jug;
• 
  `v(\text{jug}) = 2.7\; {\rm m\cdot s^(-1)}` is the velocity of the jug after the toss;
• 
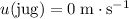  `u(\text{jug}) = 0\; {\rm m\cdot s^(-1)}` is the initial velocity of the jug, which was at rest before the toss.

Hence:

`\begin{aligned}\Delta p(\text{jug}) &= m(\text{jug}) \, (v(\text{jug}) - u(\text{jug})) \\ &= (8.0)\, (2.7 - 0)\; {\rm kg\cdot m\cdot s^(-1)} \\ &= 21.6\; {\rm kg\cdot m\cdot s^(-1)}\end{aligned}`.

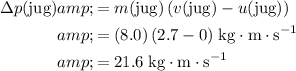Similarly, the change in the momentum of the skateboard would be:

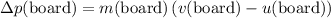`\Delta p(\text{board}) = m(\text{board}) \, (v(\text{board}) - u(\text{board}))`, where:

• 
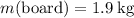  `m(\text{board}) = 1.9\; {\rm kg}` is the mass of the board;
• 
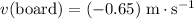  `v(\text{board}) =(-0.65)\; {\rm m\cdot s^(-1)}` is the velocity of the board after the toss;
• 
  `u(\text{board}) = 0\; {\rm m\cdot s^(-1)}` is the initial velocity of the board.

Note that the velocity of the board
`v(\text{board})\!` after the toss is opposite to that of the jug. The sign of
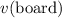`v(\text{board})` would be opposite to that of
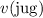`v(\text{jug})`. Since
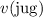`v(\text{jug})\!` is positive, the value of
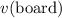`v(\text{board})\!\!` should be negative.

`\begin{aligned}\Delta p(\text{board}) &= m(\text{board}) \, (v(\text{board}) - u(\text{board})) \\ &= (1.9)\, ((-0.65)- 0)\; {\rm kg\cdot m\cdot s^(-1)} \\ &= (-1.235)\; {\rm kg\cdot m\cdot s^(-1)}\end{aligned}`.

Let
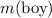`m(\text{boy})` denote the mass of the boy. The velocity of the boy was initially
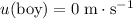`u(\text{boy}) = 0\; {\rm m\cdot s^(-1)}` and would become
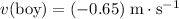`v(\text{boy}) =(-0.65)\; {\rm m\cdot s^(-1)}` after the toss. The change in the velocity of the boy would be:

`\Delta p(\text{boy}) = m(\text{boy}) \, (v(\text{boy}) - u(\text{boy}))`.

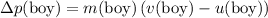Under the assumptions, the total changes in the momentum of this system (the boy, the skateboard, and the jug) should be
`0`. Thus:

`\Delta p(\text{boy}) + \Delta p(\text{boy}) + \Delta p(\text{jug}) = 0`.

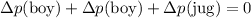Rearrange and solve for the mass of the boy:

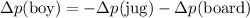`\Delta p(\text{boy}) = -\Delta p(\text{jug}) - \Delta p(\text{board})`.

`\begin{aligned} m(\text{boy}) &= \frac{-\Delta p(\text{jug}) - \Delta p(\text{board})}{v(\text{boy}) - u(\text{boy})} \\ &= (-(21.6) - (-1.235))/((-0.65) - 0)\; {\rm kg} \\ &\approx 31.3\; {\rm kg}\end{aligned}`.