Question

HELP! Find missing side lengths of B and C. Explain

Answer 1

sin30° = 1/2 = 5√2/b

b=5√2 ×2 = 10√2

tan60° = √3 = c/5√2

c=5×√2×√3

c =5√6

b = 10√2 , c = 5√6

Answer 2

`b=10√(2)\; \textsf{units}`

`c=5\sqrt6{}\; \textsf{units}`

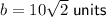
Explanation:

The interior angles of the given right triangle are 30°, 60° and 90°.

This means it is a special 30-60-90 triangle.

The measures of the sides of a 30-60-90 triangle are in the ratio 1 : √3 : 2. Therefore, the formula for the ratio of the sides is x : x√3 : 2x where:

• x is the shortest leg opposite the 30° angle.
• x√3 is the longest leg opposite the 60° angle.
• 2x is the hypotenuse opposite the right angle.

From inspection of the triangle, the measure of the shortest leg (the side opposite the 30° angle) is 5√2 units. Therefore, x = 5√2.

Side b is opposite the right angle, so it is the hypotenuse.

The hypotenuse is twice the length of the shortest leg. Therefore:

`\begin{aligned}b&=2x\\&=2 \cdot 5√(2)\\&=10√(2)\; \textsf{units}\end{aligned}`

Side c is opposite the 60° angle, so it is the longest leg of the triangle.

The longest leg is equal to the measure of the shortest leg multiplied by √3. Therefore:

`\begin{aligned}c&=x√(3)\\&=5√(2) \cdot√(3)\\&=5 √(2\cdot3)\\&=5\sqrt6{}\; \textsf{units}\end{aligned}`

In summary, the missing sides lengths b and c measure:

• 
  `b=10√(2)\; \textsf{units}`

• 
  `c=5\sqrt6{}\; \textsf{units}`