Question

This question has several parts that must be completed sequentially. If you skip a part of the question, you will not receive any points for the skipped part, and you will not be able to come back to the skipped part. A tank contains 15,000 L of brine with 22 kg of dissolved salt. Pure water enters the tank at a rate of 150 L/min. The solution is kept thoroughly mixed and drains from the tank at the same rate. Exercise (a) How much salt is in the tank after t minutes? Click here to begin! Exercise (b) How much salt is in the tank after 10 minutes? Click here to begin! Need Help? Read It Talk to a Tutor

Answer 1

a) 22e^-0.01t kilograms

b) about 19.906 kilograms

Explanation:

You want an equation for the amount of salt in a 15 kL brine tank initially containing 22 kg of salt if 150 L/min of the contents is replaced by pure water.

(a) Remaining salt

The quantity of salt s(t) in kilograms can be described by the differential equation ...

s(0) = 22; s'(t) = -150/15000·s(t)

The solution can be found by separation of variables.

`\displaystyle(ds)/(dt)=-0.01s\\\\\int{(1)/(s)}\,ds=-0.01\int{}\,dt\\\\ln(s)=-0.01t+c_1\\\\s=c_2\cdot e^(-0.01t)\qquad\text{where $c_2$ is $s(0)=22$}\\\\\boxed{s(t)=22e^(-0.01t)}`

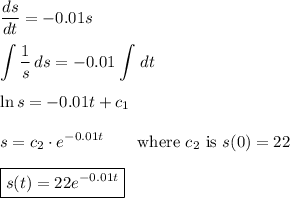
(b) s(10)

The amount of salt remaining after 10 minutes is ...

s(10) = 22·e^(-0.01·10) = 22·e^-0.1

s(10) ≈ 19.906 . . . . kilograms

There is about 19.906 kg of salt in the tank after 10 minutes.

__

Additional comment

The initial rate of change of the amount of salt is -22/100 kg/min, so after 10 minutes, we expect an approximate reduction by 2.2 kg to 19.8 kg. Since the rate slows as salt is removed, the value 19.9 kg after 10 minutes is reasonable.

There are a couple of places where the integration constant can be put in the equation for the salt quantity. As a multiplier of the exponential function, its value is found in a straightforward way.