Answer:
4/33
Explanation:
You want to write 0.1212...(repeating) as a simplified fraction.
Repeating decimal
A repeating decimal beginning at the decimal point can be made into a fraction by expressing the repeating digits over an equal number of 9s.
Here, there are 2 repeating digits, so the basic fraction is ...
12/99
This can be reduced by removing a factor of 3 from numerator and denominator:

__
Additional comment
Formally, you can multiply any repeating decimal by 10 to the power of the number of repeating digits, then subtract the original number. This gives the numerator of the fraction. The denominator is that power of 10 less 1.
0.1212... = (12.1212... - 0.1212...)/(10^2 -1) = 12/99
Doing this multiplication and subtraction also works for numbers where the repeating digits don't start at the decimal point. Finding a common factor with 99...9 may not be easy.
You can also approach this by writing the number as a continued fraction. The basic form is ...
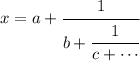
where 'a' is the integer part of the original number, and b, c, and so on are the integer parts of the inverse of the remaining fractional part. The attachment shows how this works for the fraction in the problem statement.
A calculator cannot actually represent a repeating decimal exactly, so error creeps in and may eventually become significant.