Question

The slant height of a cone measures 26 centimeters. The height of the cone measures 10 centimeters.

What is the exact surface area of the cone?
Enter your answer in the box.

Answer 1

Explanation:

To find:-

• The surface area of the cone .

Answer:-

We are here given that, the slant height of the cone is 26cm and the height is 10cm. We are interested in finding the surface area of the cone. There are two types of surface area of the cone Curved surface area and total surface area abbreviated as CSA and TSA respectively.

CSA of cone is given by :-

`\sf:\implies CSA = \pi r \ell \\`

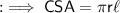
where ,

• r is the radius of the cone .
• l is the slant height of the cone.

TSA of cone is given by :-

`\sf:\implies TSA = \pi r^2 + \pi r \ell\\`

`\sf:\implies TSA = \pi r ( r + \ell )\\`

`\rule{200}2`

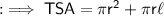
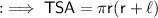
To find out the CSA we first need to find out the radius of the cone , which can be calculated using Pythagoras theorem ,

`\setlength{\unitlength}{1.2mm}\begin{picture}(5,5)\thicklines\put(0,0){\qbezier(1,0)(12,3)(24,0)\qbezier(1,0)(-2,-1)(1,-2)\qbezier(24,0)(27,-1)(24,-2)\qbezier(1,-2)(12,-5)(24,-2)}\put(-0.5,-1){\line(1,2){13}}\put(25.5,-1){\line(-1,2){13}}\multiput(12.5,-1)(2,0){7}{\line(1,0){1}}\multiput(12.5,-1)(0,4){7}{\line(0,1){2}}\put(18,1.6){\sf{r}}\put(9.5,10){\sf{h}}\put(21,11){$\sf \ell $}\end{picture}`

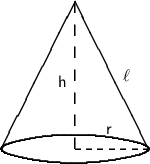
From the above diagram,

`\sf:\implies r^2+h^2=\ell^2\\`

`\sf:\implies r^2 = 26^2-10^2\\`

`\sf:\implies r^2 = 676-100 \\`

`\sf:\implies r=√(576) \\`

`\sf:\implies\pink r= 24\ cm \\`

`\rule{200}2`

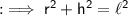
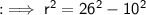
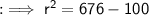
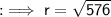
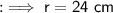
To find out the CSA , we can substitute the respective values, as ;

`\sf:\implies CSA = 3.14 * 24cm * 26cm \ \\`

`\sf:\implies \pink{ CSA = 1961.14 \ cm^2} \\`

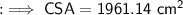
Hence the curved surface area of the cone is 1961.14cm² .

`\rule{200}2`

To find out the TSA , we can substitute the respective values as,

`\sf:\implies TSA = 3.14 (24cm)(24cm+26cm) \\`

`\sf:\implies TSA = 75.43 cm * 50cm \\`

`\sf:\implies \pink{ TSA = 3771.43 cm^2}\\`

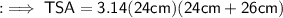
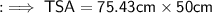
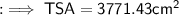
Hence the total surface area of the cone is 3771.43 cm2 .

`\rule{200}2`

Answer 2

• 1200π cm²

-----------------------------

The slant height forms a right triangle with legs being the height and the radius.

Find the radius using Pythagorean theorem:

• r² = l² - h²
• r² = 26² - 10²
• r² = 676 - 100
• r² = 576
• r = √576
• r = 24

Total surface area of the cone:

• TSA = πr(r + l)
• TSA = 24π(24 + 26) = 24π(50) = 1200π