Question

A marble is travelling at 2.0 m/s along a table top. The top of the table is 1.5 m above the floor.

Find:
a. the time the marble will take to reach the floor.
b. the distance of the table that the marble will land.
c. the velocity of the marble just before it reaches the floor.

Answer 1

time of flight = 0.5533 seconds

horizontal range = 1.107 metres

final velocity is 5.779 m/s at 70° downwards

Step-by-Step Solution

initial horizontal velocity (ux) = 2.0 m/s

initial vertical velocity (uy) = 0

vertical displacement (sy) = -1.5 m

neglecting air friction (drag), acceleration due to gravity (g) in the vertical component, is constant (9.8 m/s²), and horizontal velocity is ALWAYS constant. i.e, acceleration=0. Now using the equations of motion for the x-component:

`s=ut\\v^2=u^2\\v=u`

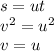
for the y-component:

`v=u-gt\\v^2=u^2-2gs\\s=ut-(1)/(2)gt^2\\`

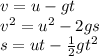
(a) the time the marble will take to reach the floor.

using an equation that we have all the data for,

`s=ut-(1)/(2)gt^2`

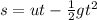
-1.5 = 0 - 1/2(9.8)×t². Solving this to get t,

∴ time of flight = 0.5533 seconds

(b) the distance of the table that the marble will land.

similar to the previous question, we can use one of the equations of motion again, but this time, there's only one equation we can use:

`s=ut`

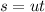
s = 2×0.5533

∴ horizontal range = 1.107 metres

c. the velocity of the marble just before it reaches the floor.

For this, we require both the x and y components of final velocity, and then we can calculate the resultant vector of the two velocities, as well as the direction/angle. Since u=v in x-component, we already have Vx. To find Vy, we can use:

`v=u-gt`

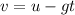
v = 0 - 9.8×0.5533

∴ final vertical velocity = -5.4223 m/s

Therefore, final velocity =
`√(Vx^2+Vy^2)`

v = √(2.0² + (-5.4223)²) = 5.779 m/s

To find direction of velocity, tan∅ = Vy/Vx

∅ = tan⁻¹(5.4223/2.0) = 70°

Therefore, final velocity is 5.779 m/s at 70° downwards