Question

Multiplying Binomials Assignment Multiply.
1. (x + 5)² ​

Answer 1

x² + 10x + 25

Explanation:

Hey!

We're using the FOIL method;

(x + 5)(x + 5) = First: x times x equals x²

Outer: x times 5 equals 5x

Inner: 5 times x equals 5x

Last: 5 times 5 equals 25

(x + 5)² = x² + 10x + 25

Therefore, (x + 5)² equals x² + 10x + 25.

Answer 2

x² + 10x + 25

Explanation:

Binomial Expansion

To expand the expression (x + 5)², we can use the formula for the square of a binomial, which states:

• (a + b)² = a² + 2ab + b²

Binomial Expansion - Calculations

In this case, we have a = x and b = 5, so we can substitute these values into the formula to get:

(x + 5)² = x² + 2(x)(5) + 5²

= x² + 10x + 25

FOIL Method

An alternative method to answering this question is using the FOIL method, which uses the following steps:

Multiply the:

1. First Terms

2. Outside Terms

3. Inside Terms

4. Last Terms

Then, add all of the terms together.

FOIL Method - Calculations

Since we are squaring (x + 5), we can multiply the expression by itself:

`(x + 5)(x + 5)`

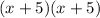
Then, we can perform the FOIL method:

First Terms

`(\underline{x}+5)(\underline{x}+5)`

`x* x=x^2`

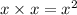
Outside Terms

`(\underline{x}+5)(x+\underline{5})`

`x* 5 = 5x`

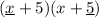
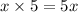
Inside Terms

`(x+\underline{5})(\underline{x}+5)`

`x* 5 = 5x`

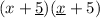
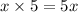
Last Terms

`(x+\underline{5})(x+\underline{5})`

`5* 5 = 25`

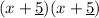
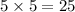
Finally, add the terms together:

`x^2+5x+5x+25`

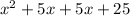
Simplify:

`\huge\boxed{x^2+10x+25}`

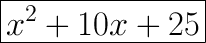
Final Answer

Therefore, the expanded form of (x + 5)² is x² + 10x + 25.