Question

How many grams of Fe2O3 can form from 27.2 g of O2?

4Fe(s)+3O2(g)⟶2Fe2O3(s)

Step 1: Show the strategy for solving this problem.
Step 2: Show the conversions required to solve this problem and calculate the grams of Fe2O3.

Answer 1

Approximately 91.14 grams of Fe2O3 can form from 27.2 grams of O2.

Step 1: Strategy for Solving the Problem

The balanced chemical equation provides a molar ratio between the reactant (O2) and the product (Fe2O3). We will use the molar ratio to convert the given mass of O2 to the mass of Fe2O3.

Step 2: Conversions and Calculations

Given:

- Mass of O2 = 27.2 g

- Balanced chemical equation:
`\(4 \text{Fe}(s) + 3 \text{O}_2(g) \rightarrow 2 \text{Fe}_2\text{O}_3(s)\)`

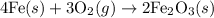
- Molar mass of O2 = 32 g/mol (from the periodic table)

- Molar mass of Fe2O3 = (
`2 * 55.85` g/mol) + (
`3 * 16.00` g/mol) = 159.7 g/mol

Conversions:

1. Convert grams of O2 to moles using the molar mass of O2.

2. Use the coefficients from the balanced equation to find the moles of Fe2O3 formed.

3. Convert moles of Fe2O3 to grams using the molar mass of Fe2O3.

Now, let's calculate:

Step 2.1: Convert grams of O2 to moles of O2.

`\[ \text{moles of O2} = \frac{\text{mass}}{\text{molar mass}} \]`

`\[ \text{moles of O2} = \frac{27.2 \, \text{g}}{32 \, \text{g/mol}} \]`

`\[ \text{moles of O2} \approx 0.85 \, \text{mol} \]`

Step 2.2: Use the coefficients from the balanced equation to find moles of Fe2O3.

The balanced equation
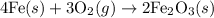`\(4 \text{Fe}(s) + 3 \text{O}_2(g) \rightarrow 2 \text{Fe}_2\text{O}_3(s)\)` shows that 3 moles of O2 produce 2 moles of Fe2O3.

`\[ \text{moles of Fe2O3} = (2)/(3) * \text{moles of O2} \]`

`\[ \text{moles of Fe2O3} = (2)/(3) * 0.85 \]`

`\[ \text{moles of Fe2O3} \approx 0.57 \, \text{mol} \]`

Step 2.3: Convert moles of Fe2O3 to grams using the molar mass of Fe2O3.

`\[ \text{grams of Fe2O3} = \text{moles} * \text{molar mass} \]`

`\[ \text{grams of Fe2O3} = 0.57 \, \text{mol} * 159.7 \, \text{g/mol} \]`

`\[ \text{grams of Fe2O3} \approx 91.14 \, \text{g} \]`

Approximately 91.14 grams of Fe2O3 can form from 27.2 grams of O2.

Answer 2

91.2 grams of
`Fe_2O_3` can form from 27.2 grams of
`O_2`.

Moles of O2:

`\[ \text{Moles of O}_2 = \frac{\text{Mass}}{\text{Molar mass}} \]`

`\[ \text{Moles of O}_2 = \frac{27.2 \, \text{g}}{32 \, \text{g/mol}} \]`

`\[ \text{Moles of O}_2 \approx 0.85 \, \text{mol} \]`

Moles of Fe2O3 formed:

According to the balanced equation, 3 mol
`O_2` produces 2 mol
`Fe}_2\text{O}_3\)`.

`\[ \text{Moles of Fe}_2\text{O}_3 = (2)/(3) * \text{Moles of O}_2 \]`

`\[ \text{Moles of Fe}_2\text{O}_3 = (2)/(3) * 0.85 \, \text{mol} \]`

`\[ \text{Moles of Fe}_2\text{O}_3 \approx 0.57 \, \text{mol} \]`

Mass of Fe2O3 formed:

`\[ \text{Mass of Fe}_2\text{O}_3 = \text{Moles of Fe}_2\text{O}_3 * \text{Molar mass} \]`

`\[ \text{Mass of Fe}_2\text{O}_3 = 0.57 \, \text{mol} * 159.7 \, \text{g/mol} \]`

`\[ \text{Mass of Fe}_2\text{O}_3 \approx 91.2 \, \text{g} \]`

Therefore, approximately 91.2 grams of
`Fe_2O_3` can form from 27.2 grams of O2.