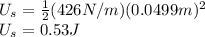Question

a spring a has a force constant of 426 n/m. if the spring is stretched 4.99 cm from the equilibrium position, then what amount of elastic potential energy is stored in the spring?

Answer 1

0.53 J

Step-by-step explanation:

We start with Hooke's law:

`F_(s) = -kx`

where k is the spring constant and x is the distance the spring is stretched from its equilibrium position.

We can integrate this to find the equation for the potential energy of a spring.

`U_(s) = -\int\limits{F_(s)} \, dx\\U_(s) = -\int\limits{F_(s)} \, dx\\U_(s) = (1)/(2) kx^2`

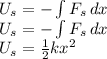
In the problem it is given:

`k = 426 N/m\\x = 4.99 cm = 0.0499 m`

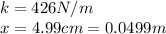
Plugging in and solving, this gives us:

`U_(s) = (1)/(2) (426N/m)(0.0499m)^2\\U_(s) = 0.53 J`