Question

What is a solution to the system of equations that includes quadratic function f(x) and linear function g(x)?

f(x) = 3x^2 + x + 3

Answer 1

Based on the given options, the solution to the system of equations that includes f(x) and g(x) is: (-2, 13) and (-1, 5)

How to find the solution to the system of equations

To find the solution to the system of equations that includes the quadratic function
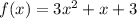`f(x) = 3x^2 + x + 3` and the linear function g(x), determine the points of intersection between the two functions.

From the given options, check which points lie on both f(x) and g(x) by substituting the x-values into the equations and verifying if the y-values match.

Let's check each option:

Option 1: (-2, 13)

f(-2) = 3
`(-2)^2` + (-2) + 3 = 12 + (-2) + 3 = 13

g(-2) = -2

The y-values match, so (-2, 13) is a possible solution.

Option 2: (-1, 5)

f(-1) = 3
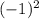`(-1)^2` + (-1) + 3 = 3 - 1 + 3 = 5

g(-1) = 3

The y-values match, so (-1, 5) is a possible solution.

Option 3: (0, 7)

f(0) = 3
`(0)^2` + 0 + 3 = 0 + 0 + 3 = 3

g(0) = 7

The y-values do not match, so (0, 7) is not a solution.

Option 4: (1, 7)

f(1) = 3
`(1)^2` + 1 + 3 = 3 + 1 + 3 = 7

g(1) = 9

The y-values do not match, so (1, 7) is not a solution.

Based on the given options, the solution to the system of equations that includes f(x) and g(x) is:

(-2, 13) and (-1, 5)

What is a solution to the system of equations that includes quadratic function f(x) and linear function g(x)? f(x) = 3x^(2) + x + 3 x g(x) -2 3 -1 5 0 7 1 9 2 11 (-2, 13) (-1, 5) (0, 7) (1, 7)