Question

Find a1 in the geometric series Sn=3045, r=2/5, and an=120 Please help this is due at 11:59 pm TONIGHT! Remember to show work!

Answer 1

a1 = 1875

Explanation:

You want a1 for the geometric series that has r = 2/5, an = 120, and Sn = 3045.

Series relations

The n-th term of the geometric series with first term a1 and common ratio r is ...

an = a1·r^(n-1)

The sum of the first n terms of the geometric series is ...

Sn = a1·(r^n -1)/(r -1)

Application

We can use the expression for an to substitute for r^n in the sum equation:

`a_n=a_1(r^n)(r^(-1))\\\\r^n=(a_n)/(a_1r^(-1))=(a_nr)/(a_1)\\\\S_n=a_1(r_n-1)/(r-1)=a1((a_nr)/(a_1)-1)/(r-1)\\\\S_n=(a_nr-a_1)/(r-1)\\\\a_1=a_nr-S_n(r-1)=a_nr+(1-r)S_n\\\\a_1=(120)(2)/(5)+(1-(2)/(5))(3045)=(2\cdot120+3\cdot3045)/(5)\\\\\boxed{a_1=1875}`

__

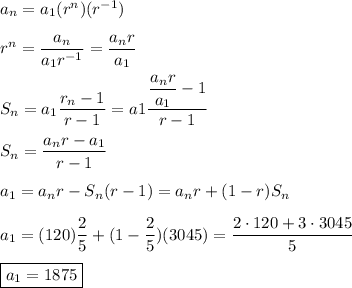
Additional comment

The sum is of the first four terms:

1875 +750 +300 +120 = 3045

We can also find this by working backward. The previous term is 5/2 times the current term. We need to find the terms that have a sum of 3045.

120 +300 +750 +1875 +4687.5 +...

Clearly, 5 terms is too many. The sum of the first 4 terms of the backward series is 3045, so we know n=4 and the first term is 1875—the last term of our 4-term backward series.