a. At equilibrium when PSO₃ = 300. atm and PO₂ = 100. atm, PSO₂ is 23.0 atm.
b. Kc is 1250 and PSO₂ is 0.0020 atm.
How to calculate PSO₂ at equilibrium
(a) To calculate PSO₂ at equilibrium, use the equilibrium constant expression and the given equilibrium concentrations of PSO₃ and PO₂.
The equilibrium constant expression for the reaction is:
![Kc = [PSO_2]^2 / ([PSO_2]^2 * [PO_2])](https://img.qammunity.org/2024/formulas/mathematics/high-school/796fzgn464gztitfy4l2wnb6dd7pc6vha3.png)
Given:
Kc = 1.7 ×
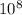
PSO₃ = 300 atm
PO₂ = 100 atm
Substituting these values into the equilibrium constant expression, we get:
1.7 ×
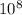 =
=
![(300^2) / ([PSO_2]^2](https://img.qammunity.org/2024/formulas/mathematics/high-school/nl4hiwbm0vtwld3uhgo3eii59vaj5s94yq.png) * 100)
* 100)
Rearranging the equation to solve for PSO₂:
![([PSO_2]^2 * 100) = (300^2) / (1.7 * 10^8)\\[PSO_2]^2 = (300^2) / (1.7 * 10^8 * 100)\\[PSO_2]^2 = 529.41]()
PSO₂ = √529.41
PSO₂ = 23.0 atm
Therefore, PSO₂ is 23.0 atm.
(b) To calculate Kc at the new equilibrium and PSO₂, use the given initial amounts of SO₂, O₂, and SO₃.
The initial moles of SO₂ = 0.0040 mol
The initial moles of O₂ = 0.0028 mol
The initial moles of SO₃ = 0 mol (since it is not given)
The change in moles for SO₂ = -0.0020 mol (since 0.0020 mol of SO₂ reacts to form 0.0020 mol of SO₃)
The change in moles for O₂ = -0.0020 mol (since 0.0020 mol of O₂ reacts to form 0.0020 mol of SO₃)
The change in moles for SO₃ = +0.0020 mol (since 0.0020 mol of SO3 is formed)
The equilibrium moles of SO₂ = initial moles of SO₂ + change in moles of SO₂
= 0.0040 mol + (-0.0020 mol)
= 0.0020 mol
The equilibrium moles of O₂ = initial moles of O₂ + change in moles of O₂
= 0.0028 mol + (-0.0020 mol)
= 0.0008 mol
The equilibrium moles of SO₃ = initial moles of SO₃ + change in moles of SO₃
= 0 mol + 0.0020 mol
= 0.0020 mol
Now, calculate Kc using the equilibrium concentrations:
![Kc = [SO_3]^2 / ([SO_2]^2 * [O_2])](https://img.qammunity.org/2024/formulas/mathematics/high-school/b42mix71g6lc1pud0so59qnbxwh75s221g.png)
Substituting the values:
Kc =
 * 0.0008)
* 0.0008)
Kc = 1 / 0.0008
Kc = 1250
The equilibrium concentration of SO₂, PSO₂, is given by the moles of SO₂ divided by the volume:
PSO₂ = moles of SO₂ / volume
= 0.0020 mol / 1.0 L
= 0.0020 M
Therefore, Kc is 1250 and PSO₂ is 0.0020 atm.
Complete question
An engineer examining the oxidation of SO2 in the manufacture of sulfuric acid determines that Kc = 1.7 multiplied by 108 at 600. K:
2 SO2(g) + O2(g) reverse reaction arrow 2 SO3(g).
(a) At equilibrium, PSO3 = 300. atm and PO2 = 100. atm. Calculate PSO2.
PSO2 = _________. atm
(b) The engineer places a mixture of 0.0040 mol of SO2(g) and 0.0028 mol of O2(g) in a 1.0-L container and raises the temperature to 1000 K. At equilibrium, 0.0020 mol of SO3(g)
K_c =
PSO2 = _________. atm