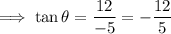Question

Please explain your answer thoroughly. I need help understanding trig

if cos∅= -5/13 and sin∅ > 0, than tan∅ is...

Answer 1

`\tan\theta=-(12)/(5)`

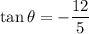
Explanation:

Given:

`\cos \theta=-(5)/(13)`

`\sin \theta > 0`

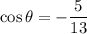
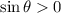
Cosine is negative in Quadrants I, II and III.

Sine is positive in Quadrant II only.

Therefore, as cos(θ) is negative and sin(θ) is positive, we need to draw a right triangle in Quadrant II.

`\boxed{\begin{minipage}{9 cm}\underline{Cosine trigonometric ratio} \\\\$\sf \cos(\theta)=(A)/(H)$\\\\where:\\ \phantom{ww}$\bullet$ $\theta$ is the angle. \\ \phantom{ww}$\bullet$ $\sf A$ is the side adjacent the angle. \\\phantom{ww}$\bullet$ $\sf H$ is the hypotenuse (the side opposite the right angle). \\\end{minipage}}`

The cosine trigonometric ratio is the ratio of the side adjacent the angle to the hypotenuse. Therefore, we can draw a right triangle where the side adjacent to angle θ is -5 and the hypotenuse is 13 (see attachment).

The side opposite the angle is positive and can be calculated using Pythagoras Theorem:

`\implies a^2+b^2=c^2`

`\implies O^2+(-5)^2=13^2`

`\implies O^2=144`

`\implies O=12`

`\boxed{\begin{minipage}{7 cm}\underline{Tangent trigonometric ratio} \\\\$\sf \tan(\theta)=(O)/(A)$\\\\where:\\ \phantom{ww}$\bullet$ $\theta$ is the angle. \\ \phantom{ww}$\bullet$ $\sf O$ is the side opposite the angle. \\\phantom{ww}$\bullet$ $\sf A$ is the side adjacent the angle.\\\end{minipage}}`

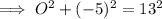
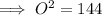
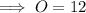
The tangent trigonometric ratio is the ratio of the side opposite the angle to the side adjacent the angle. Therefore:

`\implies \tan\theta=(12)/(-5)=-(12)/(5)`