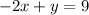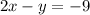Answer:
a)
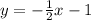
b)
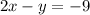
Explanation:
a)
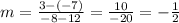
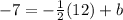

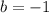
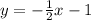
b) Slopes of perpendicular lines are negative reciprocals of each other, so if the original line has slope -1/2, the perpendicular line will have a slope of 2.
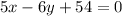
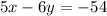
We see that the y-intercept of this line is at (0, 9), so in slope-intercept form, we have
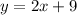
Putting this in standard form: