Question

1). A girl is three years older than her brother. The product of their ages is 54. Find their ages. 2). The breadth of a rectangle is 3m less than it's length. If the area is 180 m², find the dimensions of the rectangle.​

Answer 1

1. A girl is three years older than her brother. The product of their ages is 54.

Let's assume,

• Age of brother be x
• Age of girl be x + 3

We are given that the product of the ages of girl and her brother is 54.

`\longrightarrow x (x +3) = 54 \\ \\ \longrightarrow x^2 + 3x = 54 \\ \\ \longrightarrow x^2 + 3x - 54 = 0 \\ \\ \longrightarrow x^2 + 6x - 9x - 54 = 0 \\ \\ \longrightarrow (x +6) -9 (x + 6) = 0 \\ \\ \longrightarrow(x-9)(x + 6) = 0 \\ \\ \longrightarrow {\underline{\underline{\pink{ x = 6}}}}`

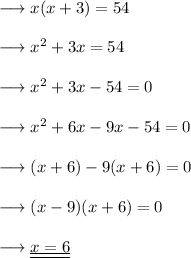
Since brother's age is x and girl's age is x + 3

Brother's age = x = 6 years.

Girl's age = x + 3

= 6 + 3 = 9 years.

Therefore, Age of girl is 9 years and her brother's is 6 years.

2. The breadth of a rectangle is 3m less than it's length. If the area is 180 m²,

Let's assume,

• Length be x
• Breadth be x - 3

We know that area of Rectangle is given by,

• Area = Length × breadth

Substituting the values,,

`\longrightarrow x(x -3) = 180 \\ \\ \longrightarrow x^2 - 3x = 180 \\ \\\longrightarrow x^2 -3x -180 = 0 \\ \\\longrightarrow x^2 + 15x - 12x -180 = 0 \\ \\\longrightarrow x(x +15) -12 (x + 5) = 0 \\ \\\longrightarrow (x -12) (x+15) = 0 \\ \\\longrightarrow {\underline{\underline{\pink{x = 15}}}} \\ \\`

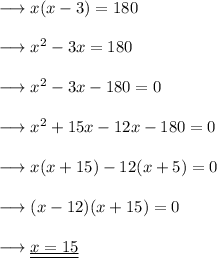
Since length is x and breadth is x -3

Substituting the values of x in length and breadth,

Length of rectangle = 15 m

Breadth of rectangle = 15 -3 = 12 m

Hence, dimensions of the rectangle are 15 m and 12 m.