Question

Write the standard form of the equation for a parabola with focus at (2, 0) and vertex at (0, 0).

Answer 1

`y^2=8x`

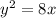
Explanation:

The axis of symmetry passes through the vertex of the parabola, and the focus lies on the axis of symmetry. Given the vertex is (0, 0) and the focus is at (2, 0), this means that the axis of symmetry is horizontal, and therefore the parabola is a sideways parabola.

The standard form of a parabola with a horizontal axis of symmetry is:

`\boxed{(y-k)^2=4p(x-h)\quad \textsf{where $p\\eq 0$}}`

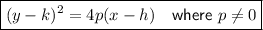
where:

• Vertex = (h, k)
• Focus = (h+p, k)
• Axis of symmetry: y = k

Given the vertex is (0, 0) and the focus is (2, 0):

• h = 0
• k = 0
• p = 2

Substitute these values into the formula to create an equation for the parabola:

`\implies (y-0)^2=4 \cdot 2(x-0)`

`\implies y^2=8x`

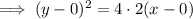
Therefore, the standard form of the equation for a parabola with focus at (2, 0) and vertex at (0, 0) is y² = 8x.