Answer:
Explanation:
Givens
- The area of a rectangular room is 750 square feet.
- The width of the room is 5 feet less than the length of the room.
Let's call
 the width and
the width and
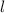 the length. According to the problem they are related as follows
the length. According to the problem they are related as follows
 , because the width is 5 feet less than the lenght.
, because the width is 5 feet less than the lenght.
We know that the area of the room is defined as

Where

Replacing the given area and the expression, we have



We need to find two number which product is 750 and which difference is 5, those numbers are 30 and 25.

Using the zero property, we have


Where only the positive number makes sense to the problem because a negative length doesn't make any sense.
Therefore, the length of the room is 30 feet.
Also, the right answers are the second choice where, the third choice and the last choice.