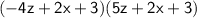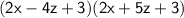Question

Factor completely and please show steps!
(2x+3)^2+(2xz+3z)−20z^2​

Answer 1

`\sf (2x-4z+3)(2x+5z+3)`

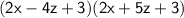
Explanation:

Given

`\sf \left(2x+3\right)^2+(2xz+3z)-20z^2`

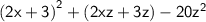
Remove the parenthesis in the second term and write the first term as a product.

`\sf \left(2x+3\right) \left(2x+3\right)+2xz+3z-20z^2`

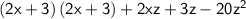
Expand the first 2 terms using the FOIL method.

`\sf \left(4x^2+12x+9\right)+2xz+3z-20z^2`

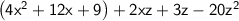
Collect in terms of
`\sf x`.

`\sf 4x^2+x(2z+12)+(-20z^2+3z+9)`

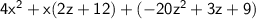
Factor out the minus sign.

`\sf 4x^2+x(2z+12)+(-(20z^2+3z+9))`

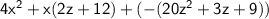
Factor
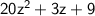`\sf 20z^2+3z+9` by finding factors of 20(-9) whose sum is
`\sf -3`.

`\sf 4x^2+x(2z+12)-(4z(5z+3)-3(5z+3))`

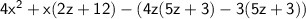
Factor common terms.

`\sf 4x^2+x(2z+12)-((4z-3)(5z+3))`

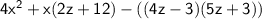
Factor the expression by splitting the product
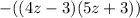`-((4z-3)(5z+3))` into two parts whose sum is
`\sf 2z+12`.

`\sf 4x^2-2x(5z+3)+2x(-4z+3)+(-4z+3)(5z+3)`

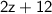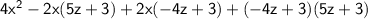
Factor by grouping.

`\sf 2x(-4z+2x+3)+(5z+3)(-4+2x+3)`

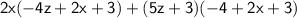
Pull a common factor out and rearrange the terms.

`\sf (-4z+2x+3)(5z+2x+3)`

`\sf (2x-4z+3)(2x+5z+3)`