Question

The aurora is caused when electrons and protons, moving in the earth’s magnetic field of ≈5. 0×10−5T, collide with molecules of the atmosphere and cause them to glow. What is the frequency of the circular orbit for an electron with speed 1. 0×106m/s? Assume that the electron moves in a plane perpendicular to the magnetic field

Answer 1

Approximately
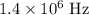`1.4 * 10^(6)\; {\rm Hz}` (assuming the effect of gravity on the electron is negligible.)

Step-by-step explanation:

Under the assumptions, the magnetic force on the electron will be:

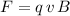`F = q\, v\, B`, where:

• 
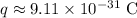  `q \approx 9.11 * 10^(-31)\; {\rm C}` is the electric charge on the electron,
• 
  `v` is the velocity of the electron tangential to the magnetic field, and
• 
  `B \approx 5.0 * 10^(-5)\; {\rm T}` is the strength of the magnetic field.

If the weight of the electron is negligible, the net force on the electron will be equal to the magnetic force:
`F_{\text{net}} = q\, v\, B`.

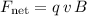Since the electron is in a circular motion, the net force on the electron would also be equal to:

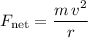`\displaystyle F_{\text{net}} = (m\, v^(2))/(r)`, where:

• 
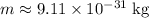  `m \approx 9.11 * 10^(-31)\; {\rm kg}` is the mass of the electron,
• 
  `v` is the orbital speed of the electron, and
• 
  `r` is the orbital radius.

Equate both sides and solve for the orbital radius
`r`:

`\displaystyle q\, v\, B = (m\, v^(2))/(r)`.

`\displaystyle r &= (m\, v^(2))/(q\, v\, B) = (m\, v)/(q\, B)`.

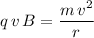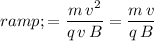The electron needs to travel a distance of
`2\, \pi\, r` in each of its circular orbit. At a speed of
`v`, each cycle will take
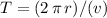`T = (2\, \pi\, r ) / (v)`. The frequency of this circular motion will be:

`\begin{aligned}f &= (1)/(T) \\ &= (1)/((2\, \pi\, r) / (v)) \\ &= (v)/(2\, \pi\, r) \\ &= (v)/(2\, \pi\, (m\, v) / (q\, B)) \\ &= (q\, v\, B)/(2\, \pi\, m\, v) \\ &= (q\, B)/(2\, \pi\, m)\end{aligned}`.

In other words, the frequency of the orbit would be
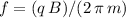`f = (q\, B) / (2\, \pi\, m)`. Note that the orbital velocity
`v` isn't part of this expression. Because the orbital radius
`r` is proportional to
`v\!`, the frequency of the motion does not depend on
`v\!\!`.

Substitute in
`q \approx1.602 * 10^(-19)\; {\rm C}`,
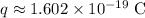`B \approx 5.0 * 10^(-5)\; {\rm T}`, and
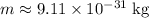`m \approx 9.11 * 10^(-31)\; {\rm kg}` into the expression and solve for frequency
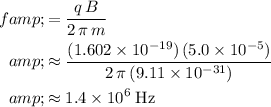`f`:

`\begin{aligned}f &= (q\, B)/(2\, \pi\, m) \\ &\approx ((1.602 * 10^(-19))\, (5.0 * 10^(-5)))/(2\, \pi\, (9.11 * 10^(-31))) \\ &\approx 1.4 * 10^(6)\; {\rm Hz}\end{aligned}`.