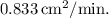The rate of change of the surface area when the radius is 12 cm is approximately
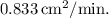
To find the rate of change of the surface area of a spherical balloon, we can use the formula for the surface area of a sphere:
![\[ A = 4 \pi r^2 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/anptksnxalp791rsaa24i7c5ayo7y4mpiq.png)
where
 is the surface area and
is the surface area and
 is the radius. To find the rate of change
is the radius. To find the rate of change
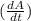 with respect to time, we take the derivative of both sides of the equation:
with respect to time, we take the derivative of both sides of the equation:
![\[ (dA)/(dt) = 8 \pi r (dr)/(dt) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/9s3oqegsqmsue16sz2e4i8bqtini3v6wc1.png)
Given that the gas is escaping the balloon at a rate of
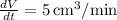 , and the volume
, and the volume
 of a sphere is
of a sphere is
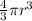 , we can relate the rate of change of volume to the rate of change of the radius:
, we can relate the rate of change of volume to the rate of change of the radius:
![\[ (dV)/(dt) = 4 \pi r^2 (dr)/(dt) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/2qcafzgouay0qytazlv6nlb84fixj7cnov.png)
Given
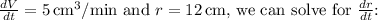
![\[ 5 = 4 \pi (12)^2 (dr)/(dt) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/iks29wua2bzr7457mymkuxa79ci5l7k3lu.png)
Solving for
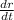 gives:
gives:
![\[ (dr)/(dt) = (5)/(4 \pi (12)^2) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/koqwex2k8pvq8u1ga48kpc0zb7zyoj91en.png)
4. Now that we have
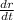 , we can use it to find the rate of change of the surface area
, we can use it to find the rate of change of the surface area
 using the formula:
using the formula:
![\[ (dA)/(dt) = 8 \pi r (dr)/(dt) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/9s3oqegsqmsue16sz2e4i8bqtini3v6wc1.png)
Substitute the known values:
![\[ (dA)/(dt) = 8 \pi * 12 * (5)/(4 \pi (12)^2) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/kocp790al2ldo4ch04jl1k9yr9m7p97t97.png)
![\[ (dA)/(dt) = (5)/(6) \, \text{cm}^2/\text{min} \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/qe0m2qddzvkmkxt3pzvzthkm2vpvyhvyfz.png)
Therefore, the rate of change of the surface area when the radius is 12 cm is approximately