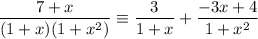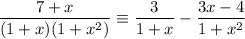Question

Resolve it into a partial fraction

Answer 1

`(7+x)/((1+x)(1+x^2))\equiv (3)/(1+x)-(3x-4)/(1+x^2)`

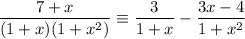
Explanation:

As the denominator has a linear factor and irreducible quadratic factor, the partial fraction form is:

`\boxed{(N(x))/((ax+b)(x^2+bx+c)) \equiv (A)/(ax+b)+(Bx+C)/(x^2+bx+c)}`

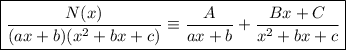
Therefore, the given algebraic fraction can be written as partial fractions of the form:

`(7+x)/((1+x)(1+x^2))\equiv (A)/(1+x)+(Bx+C)/(1+x^2)`

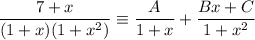
Add the partial fractions:

`(7+x)/((1+x)(1+x^2))\equiv (A(1+x^2)+(Bx+C)(1+x))/((1+x)(1+x^2))`

Cancel the denominators from both sides of the original identity, so the numerators are equal:

`7+x \equiv A(1+x^2)+(Bx+C)(1+x)`

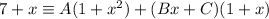
Substitute a value of x which make one of the expressions in the brackets equal zero to get rid of all but one of A, B and C.

`\begin{aligned}x=-1 \implies 7+(-1) &=A(1+(-1)^2)+(Bx+C)(1+(-1))\\7-1&=A(1+1)+(Bx+C)(0)\\6 & =2A\\3&=A\end{aligned}`

Substitute the found value of A:

`7+x \equiv 3(1+x^2)+(Bx+C)(1+x)`

Substitute x = 0 and solve for C:

`\begin{aligned} x=0 \implies 7+0 &=3(1+(0)^2)+(B(0)+C)(1+0)\\ 7&=3(1)+C(1)\\7&= 3+C\\4&=C\end{aligned}`

Substitute the found values of A and C:

`7+x \equiv 3(1+x^2)+(Bx+4)(1+x)`

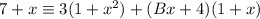
Expand the right side:

`\begin{aligned}7+x &\equiv 3(1+x^2)+(Bx+4)(1+x)\\7+x &\equiv 3+3x^2+Bx+Bx^2+4+4x\\7+x&\equiv(3+B)x^2+(4+B)x+7\end{aligned}`

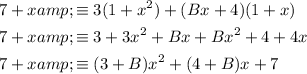
Compare the coefficients of the terms in x to solve for B:

`\begin{aligned} 1&=4+B\\-3&=B\end{aligned}`

Therefore:

• A = 3
• B = -3
• C = 4

Finally, replace A, B and C in the original identity:

`(7+x)/((1+x)(1+x^2))\equiv (3)/(1+x)+(-3x+4)/(1+x^2)`

`(7+x)/((1+x)(1+x^2))\equiv (3)/(1+x)-(3x-4)/(1+x^2)`