Question

About 3% of the population has a particular genetic mutation. 600 people are randomly selected.

Find the standard deviation for the number of people with the genetic mutation in such groups of 600. Give your answer as a decimal out to at least 4 places.

Answer 1

Standard deviation for the number of people with the genetic mutation = 4.178

Explanation:

Given random sample size 'n' = 600

proportion of the Population 'p' = 3% or 0.03

Let 'X' be the random variable in binomial distribution

Mean of the binomial distribution

`\mu = \text{n p}`

`= 600 * 0.03`

`= 18`

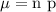
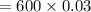
Mean of the binomial distribution ' μ ' = 18

Standard deviation of the binomial distribution

`\sigma=\sqrt{\text{npq}}=√(600*0.03*0.97) =√(17.46) =4.178`

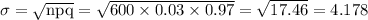
Conclusion:

Standard deviation for the number of people with the genetic mutation = 4.178