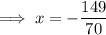Question

Solve the following logarithmic equation.
8+ log (7x+15) = 7

Answer 1

`x=-(149)/(70)`

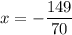
Explanation:

Given logarithmic equation:

`8+\log(7x+15)=7`

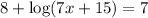
Subtract 8 from both sides of the equation:

`\implies \log(7x+15)=-1`

When the log has no base, it is the common logarithm which always has a base of 10. Therefore:

`\implies \log_(10)(7x+15)=-1`

`\textsf{Apply the log law:} \quad \log_ab=c \iff a^c=b`

`\implies 10^(-1)=7x+15`

`\textsf{Apply the exponent rule:} \quad a^(-n)=(1)/(a^n)`

`\implies (1)/(10)=7x+15`

`\implies 7x+15=(1)/(10)`

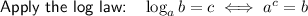
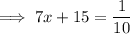
Multiply both sides of the equation by 10:

`\implies 70x+150=1`

Subtract 150 from both sides:

`\implies 70x=-149`

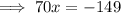
Divide both sides by 70:

`\implies x=-(149)/(70)`