Question

You deposit $7550 into an account that pays 7.25% interest, compounded continuously. How long will it take the money to triple?

Round to the nearest tenth.

Answer 1

Explanation:

It doesn't matter how much money was deposited

e^(rt) = 3 r = decimal rate interest = .0725 t = years

e^(.0725t )= 3 ln both sides

.0725 t = ln (3)

t = 15.2 yrs

Answer 2

The number of years it will take for the money to triple is 15.2 years (rounded to the nearest tenth).

Explanation:

To determine how long it will take $7550 deposited into an account that pays 7.25% interest (compounded continuously) to triple, use the continuous compounding interest formula.

Continuous Compounding Formula

`\large \text{$ \sf A=Pe^(rt) $}`

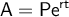
where:

• A = Final amount.
• P = Principal amount.
• e = Euler's number (constant).
• r = Annual interest rate (in decimal form).
• t = Time (in years).

Given values:

• A = 3P
• P = $7550
• r = 7.25% = 0.0725

Substitute the given values into the formula:

`\implies \sf 3 \cdot 7550=7550e^(0.0725t)`

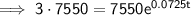
Divide both sides of the equation by 7550:

`\implies \sf 3=e^(0.0725t)`

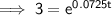
Take natural logs of both sides of the equation:

`\implies \sf \ln 3=\ln e^(0.0725t)`

`\textsf{Apply the log power law:} \quad \ln x^n=n \ln x`

`\implies \sf \ln 3=0.0725t\ln e`

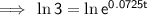
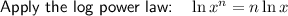
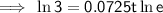
Apply the log law: ln(e) = 1

`\implies \sf \ln 3=0.0725t`

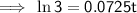
Divide both sides of the equation by 0.0725:

`\implies \sf t=(\ln 3)/(0.0725)`

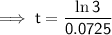
Simplify:

`\implies \sf t=15.1532729...`

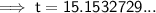
Therefore, the number of years it will take for the money to triple is 15.2 years (rounded to the nearest tenth).